Правило точности РеяИзмеряй микрометром.Отмечай мелом.Отрубай топором.
Импичмент президенту
Как ни странно, но «хитрые» задачи с экономическим или политическим подтекстом не просто возможны, но и имеют корректное математическое решение, несмотря на бросающийся в глаза метафорически–сатирический подтекст. В качестве примера, рассмотрим такую задачу:
Генеральный прокурор загадывает три двухзначных числа: $a,b,c$. Президент должен назвать ему три числа $X,Y,Z$, после чего прокурор сообщит ему сумму $aX+bY+cZ$. Президент должен отгадать все загаданные числа, иначе ему будет объявлен импичмент. Как ему спастись?
Решение этой задачи с точки зрения математики зависит от использованной системы счисления, точнее её основания, так как числа должны разделять двузначные числа, вынося их на непересекающиеся позиции системы счисления, то есть если основание системы счисления $d$, то различия между степенями $d^i$ должно быть не меньше двух.
Подразумевая использование десятичной системы и не слишком больших чисел для суммы, такой последовательностью будет $0,2,4$, что преобразуется в цепочку чисел $1,100,10000$, причём формально говоря — в произвольном порядке, только потом самому надо не запутаться в восстановлении их соответствия исходной цепочке $a,b,c$.
Площадь и минимальный периметр
В ряду прикладных задач на связь между площадью фигуры (например, пастбище для скота) и её формы дающей наименьший периметр (длина ограды пастбища) известно, что её точное решение даёт участок в форме круга и, формально, длина периметра зависит как от самой площади, числа Пи, так и требует вычисления квадратного корня. Однако мало кто даёт себе отчёт в бессмысленности этого решения на практике. Разберитесь.
Очевидно, что на практике, именно для того, чтобы избежать подобных накладок, мы всегда исходим из значения, (чуть) большего формального ответа.
Обороты колеса
Арена цирка имеет в окружности 150 метров, а размер велосипедного колеса циркового моноцикла – 20 дюймов. Сколько оборотов сделает колесо, объехав арену один раз? |
| Цирк на Цветном |
Что касается собственно задачи, то если мы хотим дать более детальную информацию, в ответе нет особой нужды упоминать кучу дополнительных цифр. Достаточно будет сказать: почти ;$94$ полных оборотов колеса. Получив такую информацию, мы будем знать, что если мы хотим совершить полный круг по арене, необходимо сделать $94$ оборотов колеса, так как $93$-х не хватит.
Игра слов: Произведение чисел
Скромные однозначные числа Пять и Семь познакомились, понравились друг другу и решили помножиться. И вот в результате появилось на свет их произведение - Тридцать Пять. Носятся сомножители со своим произведением, не могут им нарадоваться. Смотрите, - говорят соседям — это наше произведение. Ну, каково? Двузначное число, не то что мы, однозначные. А произведение и не смотрит на сомножители. Воротит нос, боится, как бы знакомые чего не подумали. Как-никак сомножители — однозначные числа, стыдно произведению иметь такую родню. Произведение давно забыло, кто его произвёл на свет. Верен ли этот рассказ для любых однозначных чисел?В данном случае это не просто забавный рассказ про числа, но и обыгрывание второго значения слова произведение: результат труда, обычно художественный. Таким образом в забавной форме мы показываем связь между лингвистикой и математикой, превращая рассказ в притчу, которая при этом сохранила все свойства чисел и арифметических операций. Тем не менее, не все пары однозначных чисел при умножении дают двузначное число, поэтому если убрать упоминание об конкретных значениях множителей, рассказ станет неверным.
Число и составляющие его цифры
Вам написали длинное число, например, из 10 цифр и попросили вычеркнуть 4 любые цифры, но так, чтобы новое число оказалось самым большим среди возможных.С точки зрения строгой и формальной математики можно потребовать сформировать все возможные комбинации и уже среди них выбрать самое большое число. Однако решение полным перебором всегда будет самым медленным. Поэтому необходимо подумать и сформировать несколько возможных правил, которые и приведут нас к решению с минимальным перебором, а желательно — осмысленным подбором из доступных вариантов.
Первая рекомендация очень проста и следует из самого понятия величины чисел: необходимо убирать самые маленькие из них. Однако если ограничиться только ей, мы совершим грубейшую ошибку, забыв о том, что мы имеем дело с позиционной записью, когда чем левее число в записи, тем больший вклад оно даёт. То есть если из 10-ти значного числа попросили удалить 4 цифры, результат всегда будет шестизначным числом и чем больше его первая (самая левая цифра), тем больше будет конечное число. Поэтому вместо первого, формального соображения первый шаг решения должен выглядеть так: начиная слева, вычёркивать цифры пока можем до достижения наибольшей цифры. Например, в последовательности $31415926$ при наличии только 4-х удалений мы не сможем достичь наибольшей цифры 9. Но чтобы получить наибольшую следующую, цифру 5, нам как раз надо вычеркнуть вначале 4 цифры из 4-х разрешённых ($3141$).
Однако в числе $2718281828459\ldots$ наибольшее достижимое число слева это 8-ка, для этого нам надо вычеркнуть три первых цифры, получая число $8281828459\ldots$ в котором мы можем удалить теперь только одну цифру правее той, на которой остановились, но меньше тех, которые находятся ещё правее. В нашем случае $2$-ка меньше $8$-ки, поэтому именно её и вычеркнем.
Очевидно, что повторяя эту процедуру просмотра–вычёркивания–сдвига вправо до исчерпания количества удаляемых цифр мы получим наибольшее возможное число.
Проценты и пропорции
Имеется арбуз массой 10 кг., который состоит на 99% из воды. Через некоторое время он усох, и стал состоять из воды на 98%. Сколько стал весить арбуз?
Типичный ученик составит пропорцию
10 кг - 99%
х кг - 98%
и выдаст ответ примерно 9.9 кг., что совершенно неправильно. Дело в том, что вторая составляющая арбуза, именуемая сухим веществом никуда не делась. Если изначально воды было 99%, то сухого вещества — 1%, то есть 0.1кг. После усыхания сухое вещество стало занимать уже $2\%=100\%-98\%$. То есть 0.1кг. занимают 2% новой массы арбуза и пропорция станет
10 кг - 1%
х кг - 2%
Решаем её и получаем, что масса арбуза после усыхания стала 5 кг.
В данной задаче показывается, что основой для составления пропорции должны быть неизменные количества. Ошибка типичная, всегда приводящая к ошибочному результату.
Меряем удава в удавах, а не в попугаях!
 |
| https://www.youtube.com/watch?v=XDTCc6RBJeU (все серии) |
Лохнесское чудовище имеет в длину 20 м и ещё половину своей длины. Чему равна его длина?
Кажется, что нужно сделать так: двадцать и половина от двадцати — итого тридцать. Значит, Лохнесское чудовище имеет в длину 30 м. Но как же так, разве можно иметь длину 20 и 30 метров одновременно!?
На самом деле условие задачи означает что длина Лохнесского чудовища равна сумме 20 м и половины его длины. Алгебраически это записывается как $х=20+\frac{х}{2}$, откуда $х=40$ метров.
Можно придумать и иные задачи на том же принципе. Например: кирпич на одной чаше весов уравновешен на другой чаше ¾ кирпича и гирей в ¾ кг. Чему равна масса кирпича?
Уравнение для этой задачи будет иметь вид $х=\frac{3}{4}х+\frac{3}{4}$, следовательно $х=3$ кг.
Для закрепления принципа решите задачу, использующую как основное другое арифметическое действие: «Сколько весит этот мешок картошки?» — спросил покупатель. «50 килограммов раздели на половину его собственного веса». — ответил торговец. Так сколько весил мешок картошки?
Здесь уравнение имеет несколько уровней
$\large x=\frac{50}{\frac{x}{2}}$, $x^2=100$, откуда $x=10$ кг.
Удвоение чёрного кота
Если чёрный кот дважды пересёк вам дорогу пройдясь туда-сюда, он отменил неприятности или удвоил?
Если кот векторный, то отменил, если скалярный, то удвоил.
 |
| Скаляр и вектор |
При всей шуточности вопроса, он имеет под собой однозначную связь с физическим процессом — движением и его логическим аналогом в математике — сложением. Но так как движение имеет направление, то ответ обретает строгий математический смысл.
Иррациональность не помеха
В эпоху компьютеров, калькуляторов и прочих умных устройств вычисление «неудобных» выражений включающих иррациональные числа не является помехой. Но если всё таки надо оценить примерное значение выражения, да ещё и в уме? Сделайте это для дроби $\frac{3}{\sqrt{5}}$.
 |
| Небольшая математическая хитрость |
Покупки в долг
Допустим, я взял у своего друга взаймы 100 рублей, пошёл в магазин с ними, но к несчастью их потерял. На обратном пути встретил подругу и занял у неё 50руб, вернулся в магазин, купил 2 шоколадки по цене 10 рублей каждая. Оставшиеся 30 рублей вернул другу и, следовательно, остался должен ему 70 рублей, а подруге 50 рублей. В итоге получаем $70+50=120$руб. Не забудем про две шоколадки и всего получим 140рублей. Но почему-то возникает разница $150-140=10$ руб. Где эти 10 рублей? Помогите разобраться.
Достаточно указать две грубейшие ошибки, полученные при проверке суммы долга. Складывая $70 + 50$, мы не учитываем возращённые 30 рублей. Поэтому сравнивать нужно с остатком долга в 120 руб. Если же всё-таки долг остаётся в 150 рублей, то 30 рублей друг должен нам отдать обратно. Однако вместо того чтобы их прибавить, мы добавляем 20 шоколадных рублей, которые уже учтены при сложении 70 и 50. Получается, что 20 рублей подсчитаны дважды и вместо возвращения 30 рублей к 120 рублям добавляем 20 уже учтённых. Вот Вам и разница в 10 рублей по сравнению с полной суммой. Для того чтобы запутать читателя и замаскировать ошибку, производят вычисления на тех же самых числах, только вместо того, чтобы в определённый момент выполнить сложение, меняют его на вычитание (или наоборот) и загоняют решающего в весьма трудное положение, ибо логика подбора действия на первый взгляд кажется безупречной.
Не раскрывая скобки
Решите следующее уравнение, не раскрывая скобки:
$(12x - 1)(6x - 1)(4x - 1)(3x - 1) = 5$
На примере этой математической задачи мы покажем, как часть решений можно отыскать при помощи смекалки, вернее наблюдательности, а для поиска оставшихся нужно осознать, что между значениями могут существовать дополнительные связи. Причём известные давно, но так как ими пользуются редко, то их можно отнести к «экспертным» и «обычному человеку» требуется ознакомиться с куда большим пластом информации, присутствующей в специальной литературе или закопанной внутри специализированных публикаций и/или обсуждений.
Для нашего примера видно, что часть его корней похоже связано с числом 12 и его разложением на множители, при этом должны оставаться целыми или рациональными числами (коэффициент справа). Для этого сделаем замену $x = y/12$ и после упрощения получим выражение
$(y - 1)(y - 2)(y -3)(y - 4) = 120 = 2\cdot 3\cdot 4\cdot 5$
представляющее собой произведение четырёх последовательных чисел. Причём для сохранения положительного знака произведения все четыре числа должны быть либо положительным, либо отрицательными. Отсюда следует, что два корня $-1$ и $6$ как раз и зададут такую последовательность множителей, порождая два корня исходного уравнения $-\frac{1}{12}$ и $\frac{1}{2}$.
И теперь как раз наступает момент, когда запрет раскрытия скобок не позволяет свести многочлен четвёртой степени к квадратному. И только хорошо учившийся в школе вспомнит, что была такая теорема Виетта, согласно которой между корнями квадратного уравнения и коэффициентами соответствующего многочлена существует однозначная связь, использующая только арифметические операции. Так может подобная связь существует и для многочленов больших степеней? На самом деле, найти эту связь сможет и современный троечник, если он воспользуется интернет поисковиком увязав ключевые слова в вопрос типа: «связь корней полинома и коэффициентов многочлена», а ещё лучше — употребляя вместо русскоязычного слова «многочлен» его интернациональный аналог — термин «полином». Имеются многочисленные ссылки на соответствующую алгебраическую теорему, причём на основных языках мира точно. Включая примеры. Самостоятельно ознакомьтесь с теоремой и убедитесь, что для двух оставшихся корней будут верны условия:
 |
| Теорема Виетта |
откуда следует, что оставшиеся два корня — комплексные числа. Но формально корней у исходного многочлена четыре и если уж вы вычислите эти y, не забудьте пересчитать в начальные
Неквадратный квадрат
Докажите, что произведение четырёх последовательных целых чисел плюс единица даёт полный квадрат.
Задача, которая звучит куда страшнее чем решается, если не пытаться образовывать многочлен четвёртой степени, а поискать совпадения:
 |
| Последовательность эквивалентных преобразований |
Подобный пример просто необходим среди «странных» задач как напоминание того, что в задачах с явным математическим основанием для появления многочленов четвёртой или выше степени, стоит попробовать выделить один или несколько сомножителей в разложении, но не выше кубических.
Разбитые грампластинки
Однажды, когда Боб и Элен проезжали мимо магазина грампластинок, Боб задал Элен вопрос.
Боб. Ты все ещё собираешь пластинки с джазовой музыкой?Элен. Нет, половину всех пластинок и ещё полпластинки я подарила Сьюзен.Элен. Половину оставшихся пластинок и ещё полпластинки я подарила Джо.Элен. После этого у меня осталась одна пластинка. Я подарю её тебе, если ты скажешь, сколько пластинок было у меня в коллекции до того, как я начала её раздавать.
На самом деле нас интересует в чём секрет Элен?
Попытка прямого прочтения текста диалога приведёт к естественному вопросу: «Зачем ломать пластинки, да ещё и дарить потом их обломки?» Но всё обретает смысл если вспомнить что деление нечётного числа пополам порождает целое с половинкой. Добавив к нему отсутствующую половинку как раз и получим целое число. После этого задачу можно начать решать от конца к началу, получая что Джо подарили две пластинки, а Сьюзен — четыре. То есть сначала у Элен было семь пластинок.
Ценность этой задачи именно в скрытом оперировании свойствами целочисленного деления, хотя для неё можно составить алгебраическое уравнение
 |
| "Читаем" то, что сказала Элен |
Поливаем огород
На поливку огорода длиной 35 м и шириной 12 м пошло 14 бочек воды. Сколько бочек потребуется, чтобы полить огород длиной 25 м и шириной 24 м?
Данная задача привязана к выполнению решения стандартно, то есть пошагово и возможностью записать его в виде меньшего количества действий, сгруппировав изменившиеся элементы и потом соотнести их с ориентиром. В нашем случае надо понять, как соотносится новая площадь огорода со старой:
$\large\frac{25\cdot 24}{35\cdot 12}=\frac{5\cdot 2}{7\cdot 1}=\frac{10}{7}>1~.$
И уже это число умножить на исходное количество воды: $\frac{10}{7}\cdot 14 = 10\cdot 2=20$ бочек. Таким образом, вместо подсчёта площадей и расхода воды на квадратный метр с получением неудобных дробей или вообще иррациональных чисел, мы можем записать результат в одном, или максимум в двух шагах, сохранив полный контроль над логикой решения задачи.
Поиск симметрии в графическом представлении информации дело более чем обычное. Но при работе с числовыми данными это может быть затруднено, так как симметрия подразумевает некоторое аналитическое преобразование (существование формулы). В данной задаче предполагается простое преобразование — единственное умножение. Ознакомившись с решением, оцените для себя, сможете ли Вы заметить подобные зависимости без отсутствия каких-либо подсказок?
Итак, пусть данное число равно $a + 10b + 100c + 1000d$. Тогда, по условию
Разберёмся сначала с разрядом $c$, предположив что он ненулевой. Тогда
Множим симметрию
В результате умножения на 9 порядок цифр некоторого четырёхзначного числа меняется на обратный. Найти это число.Поиск симметрии в графическом представлении информации дело более чем обычное. Но при работе с числовыми данными это может быть затруднено, так как симметрия подразумевает некоторое аналитическое преобразование (существование формулы). В данной задаче предполагается простое преобразование — единственное умножение. Ознакомившись с решением, оцените для себя, сможете ли Вы заметить подобные зависимости без отсутствия каких-либо подсказок?
Итак, пусть данное число равно $a + 10b + 100c + 1000d$. Тогда, по условию
$9\cdot (a + 10b + 100c + 1000d) = 1000a + 100b + 10c + d~.$
Причём $d$ отлично от нуля, так как это ведущий разряд исходного числа. Приведём подобные слагаемые, получив отношение $991a + 10b - 890c - 8999d = 0$. Само наличие слагаемых с разными знаками подсказывает, что стоит рассмотреть это равенство в виде $991a + 10b = 890c + 8999d$, которое фактически группирует ожидаемо большую суммы против ожидаемо меньшей.Разберёмся сначала с разрядом $c$, предположив что он ненулевой. Тогда
 |
| Оценки величин |
Эти числовые отрезки не пересекаются, значит $c=0$. Если при этом $d>1$, то правая часть равенства заведомо больше левой и единственное допустимое значение $d=1$. Следовательно $991a + 10b = 8999$. Чтобы сумма оканчивалась на $9$, необходимо $a=9$. Тогда $b=8$ и исходное число равно $1089$, а «симметричное» к нему это $9801$.
Ускорение повторных вычислений
При записи математических выражений зачастую мы их записываем по мере построения и если нам необходимо произвести одно–два вычисления, то мы просто вместо переменных подставляем числа и проводим вычисление как есть, с учётом приоритета операций и скобок, обычно слева направо. Однако если необходимо выполнить это вычисление десятки, а иной раз десятки тысяч раз, трудоёмкость вычислений, то есть количество выполняемых арифметических действий хочется сократить. Как этого добиться вообще, проиллюстрируйте на примере выражения $ac -da + bd - cb$. |
| Как лучше использовать повторяющиеся элементы? |
 |
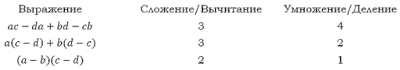| Таблица количества требуемых арифметических операций |
Понятно, что размер экономии может быть разным, но если договорится считать операции умножения и деления более долгими, то экономия даже одного из них уже даст выигрыш при повторных вычислениях. Задачи подобной оптимизации были обязательными до конца XX века, когда фактически все процессоры стали производить все арифметические операции одинаково быстро. Но даже в этих условиях есть заметная разница между семью и тремя операциями.
Строй новобранцев
Бравому солдату Швейку приказали выстроить новобранцев в ряд, чтобы офицер мог произнести перед ними речь. Нужно построить их таким образом, чтобы минимизировать среднюю разницу в росте между новобранцами, стоящими рядом. Швейк поставил самого высокого первым, самого низкого — последним, а остальным велел встать между ними кто как захочет. Выполнил ли Швейк приказ? А как бы вы выстроили новобранцев?
Швейк понял суть приказа следующим образом: нужно минимизировать выражение
$\large\frac{1}{n}\left[\left(h_2-h_1\right)\left(h_3-h_2\right)+\ldots+\left(h_{n-2}-h_{n-1}\right)+\left(h_{n-1}-h_n\right)\right]=\frac{1}{n}\left[h_n-h_1\right]$
где $n$ - количество новобранцев, а $h_i, i = 1,2,\ldots,n$ это рост новобранца, занимающего в строю $i$-ю позицию. Поскольку $h_n - h_1$ может быть отрицательно, то минимизировать его — значит сделать эту величину отрицательной с наибольшим абсолютным значением. Этого можно достичь если $h_n$ — последний солдат самый низкий, а $h_1$ — первый солдат самый высокий; рост остальных людей в выражении не учитывается, то есть они могут встать в любом порядке.Приказ, конечно же, был другим: минимизировать среднее абсолютное значение разности в росте стоящих рядом людей, то есть:
$\large\frac{1}{n}\left[|h_2-h_1|+|h_3-h_2|+\ldots+|h_{n-2}-h_{n-1}|+|h_{n-1}-h_n|\right]$
так как $n$ фиксировано, то множитель $\frac{1}{n}$ можно не учитывать. Вторая сумма минимальна, когда значения роста отсортированы по возрастанию или убыванию. Только тогда разница $h_\mathrm{max} - h_\mathrm{min}$ будет минимальна.
Эта задача иллюстрирует одну частую ошибку при решении практических задач, когда забывают, что любой аналог расстояния может быть только неотрицательным значением и задача решающего состоит именно в том, чтобы понять, идёт ли о нём речь. Так что фраза «минимизировать … разницу в росте» недостаточно строга и только опыт решающего может подсказать правильную трактовку.
Одна из тех задач, которые в рамках прямого применения арифметических свойств приведут «почти к ответу», вызвав раздражение и не научив ничему полезному. Эффект «Ага!» в этой задаче посетит только тех, кто совместит сначала сумму нескольких элементов с понятием арифметического среднего, а последнее — с геометрическим средним. А именно, для положительных чисел верно
Эта задача иллюстрирует одну частую ошибку при решении практических задач, когда забывают, что любой аналог расстояния может быть только неотрицательным значением и задача решающего состоит именно в том, чтобы понять, идёт ли о нём речь. Так что фраза «минимизировать … разницу в росте» недостаточно строга и только опыт решающего может подсказать правильную трактовку.
Среднее, оно такое среднее!
Докажите, что $\forall a,b,c>0$ выполняется $\large(a+b+c)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge 9$.Одна из тех задач, которые в рамках прямого применения арифметических свойств приведут «почти к ответу», вызвав раздражение и не научив ничему полезному. Эффект «Ага!» в этой задаче посетит только тех, кто совместит сначала сумму нескольких элементов с понятием арифметического среднего, а последнее — с геометрическим средним. А именно, для положительных чисел верно
 |
| Соотношение средних |
Следовательно, верны одновременно
Перемножая почленно и перенося численную часть сразу направо, получим
доказав неожиданное неравенство. Более того, для произвольного количества слагаемых получим
Комментарии
Отправить комментарий