Мыслим #7 Бесконечно большие, малые и «странные» величины

Закон Мерианна
Находишь всегда то, что не искал.

Труба Торричелли или рог Габриэля

Никакой краски не хватит чтобы закрасить область, ограниченную кривой y=1/x и осью x правее точки x=1 однако если эта кривая образует тело вращения, то его объём конечен и равен Пи. Разве так может быть?

Элементарное и прямое вычисление доказывает это:

Эта геометрическая странность, когда площадь внутреннего сечения фигуры вращения оказывается бесконечной, то есть нужно бесконечное количество краски на эту «стену». А простыми словами — её невозможно закрасить. При этом полный (идеальный) объём оказывается конечным.

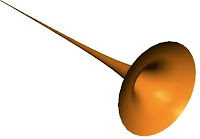рог Габриэля

Для нас это очередной пример способный показать разницу между «практико–физической» и «теорико–математическими» вселенными.

Данную задачу можно продолжить, так как при конечности объёма оказывается, что площадь поверхности этого тела вращения

опять оказывается бесконечной.

Но главным в этой задаче являются не математические вычисления с чередующимися бесконечными и конечными значениями. А сам парадокс, что конечный объём краски заполнит рожок полностью, при этом её не хватит чтобы закрасить поверхность - ведь её площадь бесконечна!!!

Как как может существовать подобное противоречие?

Бесконечная гостиница

Если все номера в гостинице с бесконечным количеством номеров заняты, можно ли подселить в неё ещё людей? Сколько?

В неё в любом случае можно поселить ещё людей, и их число может быть бесконечным. Поскольку рассуждения в этом доказательстве просты, но интересны, приведём его полностью.

• Если приехал ОДИН новый постоялец, переселим каждого имеющегося постояльца в комнату с номером на единицу большим. Теперь комната с номером 1 освободилась и туда как раз и поселим нового постояльца.
• Если приехало несколько постояльцев, например ТРОЕ. В этом случае управляющий попросил имеющихся постояльцев переселиться в комнаты с номером больше текущего на ТРИ, и за счёт этого освободил три первых для новых постояльцев.
• Если приехало бесконечное количество новых постояльцев, то управляющий попросил переселиться имеющихся в комнаты с номерами равными начальному умноженному на два. То есть старые постояльцы оказались в комнатах с чётными номерами (а их бесконечное количество), при этом все комнаты с нечётными номерами (их тоже бесконечное количество) освободились и их как раз достаточно для новых постояльцев.

В этом парадоксе объясняется, что законы логики абсолютно неприемлемы к свойствам бесконечности, хотя с конечными числами работать проще. Они не требуют хитростей.

Бесконечный периметр

Не требуется особенных знаний, чтобы понимать что у неограниченно большой фигуры действительно будет бесконечный периметр. Но может ли он быть бесконечным у ограниченной фигуры?

Если Вы попытаетесь ответить на этот вопрос оперируя категориями классической геометрии, то не сможете продвинуться, так как последняя предполагает «некую регулярность» фигур, когда странных, неповторяющихся, сильно изломанных участков мало. На самом деле упоминание об изломанности и неповторимости служит подсказкой: может именно у таких фигур самые обычные характеристики становятся странными? Совсем недавно мы видели подобное поведение у трубы Торричелли, когда одни характеристики давали конечное число, другие — бесконечность.

В явном виде этот вопрос о бесконечности конечного возник при решении практической проблемы: «Как вычислить длину побережья острова типа Британского?» Очевидно, что остров как реальный физический объект можно соотнести с фигурой, спроектированной на плоскость. Её контуры будут тем сложней и изрезанней, чем более подробна карта (меньше масштаб).

Отрезки по 100 км, оценочная длина 2800 км.

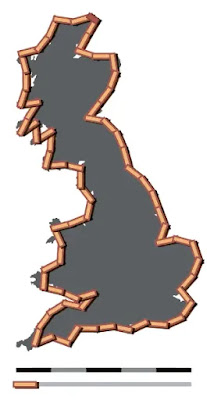Отрезки по 50 км, оценочная длина 3400 км.

Из-за изрезанной и нерегулярной траектории побережья единственной практически применимой технологии измерения стало «оконтуривание» отрезками прямых, когда траектория реального побережья заменяется замкнутой ломаной линией. Чем детальней карта, тем более короткие отрезки можно использовать. Начав эту работу, исследователи сразу столкнулись с интересным фактом: чем детальнее становился контур, тем больше становилась длина периметра соответствующей кривой. Причём последовательность оценок была строго возрастающей!

Совершенно естественно вопрос перешёл из практической плоскости в теоретическую:

Периметр "огибающей ломаной линии"
в зависимости от длины элементарного отрезка

С точки зрения логики и фактов чем короче отрезки на контуре, тем точнее описывается береговая линия. Вычислить этот предел можно на основе элементарного логико–геометрического построения. А именно надо разделить каждый из отрезков на две части, но точка разделения не должна остаться на нём. Мы сдвигаем её в сторону, образуя лучшее приближение формы берега за счёт двух новых сторон условного треугольника. При этом, согласно неравенству треугольника для длин сторон имеем

Правило треугольника

То есть проведя разбиение имеющихся отрезков, вычисление уточнённого периметра по сторонам треугольника всегда даст строго большее число и это верно всегда. Значит длина периметра не ограничена сверху и этот предел равен <плюс бесконечности>.

Таким образом мы доказали, что существуют ограниченные фигуры, у которых длина периметра бесконечна. Однако к вопросу измеримости длины береговой линии можно подойти даже более обще, так как в отличии от абстрактной геометрической фигуры береговая линия острова или материка зависит от внешних «событий». А именно, на планете у которой есть хоть один спутник достаточно близко, будут наблюдаться приливные явления. И для островов подразумевается, что приливный эффект одинаков со всех сторон. Соответственно в отлив площадь надводной поверхности будет больше, значит и периметр должен быть больше. В прилив, наоборот, часть побережья скроется под водой и значит периметр должен стать меньше. В самом общем смысле получается, что оставаясь ограниченной, размер фигуры и её внешние очертания непостоянны, то есть говорить о периметре как единственном числе нельзя в принципе. А вместе с предыдущим фактом теоретически мы говорим о числе из интервала

[Чуть меньшая бесконечность, Чуть большая бесконечность]

Сама постановка подобных задач не имеет смысла в рамках классической математики.

Если подвести итог в вольной форме, то получится что задача об измерении длины береговой линии не имеет ни практического, ни теоретического решения.

Слишком много предков

У меня есть отец и мать. У моего отца и у моей матери тоже, конечно, были отец и мать. Значит, восходя к 3-му поколению, я нахожу у себя четырёх предков. Каждый из моих двух дедов и каждая из моих двух бабушек также имели отца и мать. Следовательно, в 4-м поколении у меня 8 прямых предков. Восходя к 5-му, 6-му, 7-му и т. д. поколению назад, я нахожу, что число моих предков возрастает и притом чрезвычайно сильно. А именно как степенная последовательность двойки, давая к 20-му поколению больше полумиллиона предков. Проектируя длительности жизни даже на строго подтверждённую длительность истории человечества получим цифры с гигантским количеством нулей. Но ведь у вас, читатель, было столько же прямых предков. Прибавьте их к моим и присоедините ещё предков всех своих знакомых, да прибавьте ещё предков всех вообще людей, живущих на земле, — и вы легко вообразите себе, в каком страшно затруднительном положении были все наши предки: ведь для них буквально не хватало места на земном шаре! Так ли это было в действительности? Где в нашем рассуждении мы совершили ошибку?

Нелепый результат, который мы получили, исчисляя своих предков, объясняется тем, что мы упустили из виду одно весьма простое обстоятельство. Мы совсем не приняли в расчёт, что наши отдалённые предки могут быть в кровном родстве между собой и, следовательно, иметь общих предков. Мой отец и моя мать, быть может, уже в-5-м пли 6-м поколении назад имели общего деда. Это соображение разбивает все наши расчёты и уменьшает несметные полчища наших отдалённых предков до весьма скромной цифры.

Более того, исследуя человеческое ДНК исследователи обнаружили что несколько раз за историю человечества количество предков резко уменьшалось, на 70–90%. Исследования выявили по крайней мере два момента, когда численность человечества падала ОЧЕНЬ СИЛЬНО!

Примерно 1.2 миллиона лет назад в эпоху высокой вулканической активности и изменений климата население Земли уменьшилось до 10–18 тысяч человек. Второй раз это случилось примерно 70 тысяч лет назад из-за резкого потепления и тотальной засухи. В этот момент численность населения упала примерно до 2-х тысяч человек всего!