Закон Хатчисона
Необходимости концентрированного внимания всегда сопутствует непреодолимое желание отвлечься.
Упрощение выражений
Кажется, что последовательность выражений на картинке правильная, но в один момент символьное упрощение грубо нарушает правила арифметики в условиях задачи и это приводит к неправильному результату. Найдите и объясните эту ошибку.
Так как $a=b$ то $a-b=0$. При переходе от 4-й к 5-й строке мы сокращаем на $a-b$, что возможно символьно. Однако это действие соответствует делению на ноль обеих частей равенства, что нарушает правила арифметики и делает все последующие преобразования неверными. На самом деле эта «невидимая» ошибка: сократить одинаковые компоненты формально, без проверки их реальных значений и их допустимости возможна и в других областях знаний.
2 ? 2 = 4
$2\cdot 2 = 4$ и $2 + 2 = 4$. Это единственный пример, когда сложение и умножение двух одинаковых целых чисел даёт одинаковый результат. Но верно ли это для всех чисел?
Подобный результат дают многие пары из целого и дробного числа, например
$\large 3~\mathrm{и}~1\frac{5}{10},~4~\mathrm{и}~1\frac{1}{3}.$
Для нас этот забавный математический факт должен напоминать, что результат часто зависит от ограничений (класс чисел в задаче) или, выражаясь на современном языке — контекстно зависим.
Слон и комар
Один любитель математики путём преобразований алгебраических выражений сумел доказать, что два разных значения равны, словно слон и комар весят одинаково. Проверьте цепочку его рассуждений и найдите ошибку: Пусть x — вес слона, а y — вес комара. Обозначим сумму этих двух весов $2v$, то есть $x+y=2v$. Это же выражение можно записать в двух видах
$x-2v=-y~\mathrm{или}~x=-y+2v.$
Перемножим их почленно $x^2-2vx=y^2-2vy$ и добавим $v^2$ к обеим частям
$x^2-2vx+v^2=y^2-2vy+v^2$, откуда ${(x - v)}^2 = {(y - v)}^2$.
Извлекая квадрат и исключая $-v$, получим что $x=y$, то есть вес слона равен весу комара.
Основную ошибку любитель допустил, извлекая квадрат и забыв о втором варианте $x-v=-(y-v)$, который возвращает нас к исходному выражению $x+y=2v$. Скорее всего это означает, что $x-v$ не может равняться $y-v$ в ограничениях задачи. А именно величина v на самом деле представляет собой среднее арифметическое и в начальном предположении что x и y разные, мы имеем один из двух вариантов:
чего конечно быть не может.
5 = 1?
Как ни странно, но если знак равенства применять в рамках модульной арифметики, то 5 mod 4 = 1 и никакой ошибки нет. Однако если записать следующую цепочку преобразований, то получается что 5 = 1 всегда. Как так?
Использование знака равенства в математике не раз вызывало проблемы, так как он имеет по крайней две основных трактовки: а) равенство значений и б) результат математического действия. Обе эти трактовки должны быть действительны на всех этапах преобразования, только тогда можно гарантировать, что истинность/ложность конечного выражения означает то же самое для исходного. В приведённом рассуждении знак равенства больше всего рассматривается как результат действия, именно поэтому промежуточное выражение $2=-2$ проходит как допустимое, так как мы получили его в результате корректно проделанной операции вычитания. Да и после выполняем возведение в квадрат корректно.
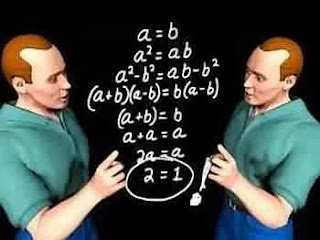


Комментарии
Отправить комментарий