Ни два, ни полтора?

О пословицах и поговорках - словно как о мёртвых: или хорошо или ничего. Очень важное и интересное явление живого языка, и, на самом деле - несомненная помощь в обучении и воспитании. При этом я всегда считал, что образ или мысль который они должны передать должен быть максимально понятным, даже если "тема" не самая простая и понятная.

Ну, математику в таком случае уж точно можно считать неудобной темой. Но если посмотреть коллекции пословиц и поговорок, то они в основном привязаны к конкретным числам и их прямым или скрытым смыслам, типа "Один в поле не воин". Но не к самому числу или его чисто математическому смыслу.

Поэтому некоторые "более" математические поговорки вызывают вопросы, так как тут приходится задуматься о том, почему именно такая "комбинация" слов для выражения общепринятого толкования.

Например - "Ноль без палочки" говорят о никчёмном, бесполезном человеке. Если привязка к значению нуля понятна, то отсутствие палочки заставляет задуматься, а это-то к чему? Наверняка есть варианты трактовок, но для меня это звучит как дополнение что никак не привязано к единице. А связано с тем, что палка = стержень. То есть мы говорим не просто о бесполезности такого человека в плане результатов его деятельности или присутствия, но и об отсутствии в нём стержня. То есть всё-таки не просто бесполезный, а именно никчёмный человек.

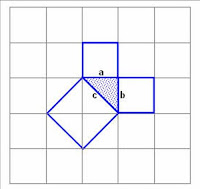
Поговорку про "Пифагоровы штаны во все стороны равны" о теореме Пифагора про прямоугольный треугольник слышали многие, но не все дали себе отчёт о её геометрической интерпретации (см. рисунок) и соответственно об образно-мнемонической подсказке-напоминании о сути формулы.

Или другая пословица с основой в житейском смысле двух ключевых слов: "Будет проще жить, если будешь друзей умножать и радость делить" - находить друзей много, может даже быстро и надолго. Плюс делиться хорошим с другими, чтобы и они так же поступали с тобой, то есть радость и добро к тебе от друзей вернётся.

Но вот с поговорками типа "Ни два, ни полтора" с ходу разобраться не получается. Звучит не как поговорка, а как загадка. Если число не целое и не рациональное, то остаётся один вариант - иррациональное число с его "странностью", то есть наличием непривычных черт и, на самом деле, бесконечной непредсказуемостью. То есть если о странности и непредсказуемости - то поговорка звучит забавно, но всё равно "для своих". Даже в эпоху всеобщего образования я, как препод с стажем уверен что большинство про иррациональные числа вспомнит далеко не сразу, а уж об их символизме вообще мало кто задумывался.

Хм.... Но звучит-то красиво!