На абстрактно–логическом уровне внешняя информация описывается так же, как и молекулы знаний, но вот её распространение внутри потока по направлению от стен к центру и «устойчивость» студента к её «потреблению» требуют особого внимания.
 |
| Ни один педагог не хочет оказаться в такой ситуации. Да и стратегия "вдалбливания" только формально относится к техникам замещения и подмены интереса |
С «устойчивостью» один из факторов очевиден: чем ниже мотивация, тем выше вероятность поглощения такой молекулы. Но если для «полезных» знаний нет разницы в их происхождении, то эффект поглощения «вредных» должен влиять на частицу–ученика по-другому.
На данный момент мы описываем молекулу знаний триадой <заряд, масса, тип> чтобы отразить изменения в заряде, объёме и плотности частицы. Поэтому, полезные они были или нет, но формально знания потреблены, и масса частицы должна быть скорректирована. Причём как обычно, так как разделение на полезные или вредные может быть ученику неизвестно и с формальной точки зрения объём и/или глубина его знаний изменились.
Значит вредность проявится в том, что заряд частицы или «запас сил» пострадает сильнее. Вместе с предполагаемой повышенной привлекательностью такой информации это означает, что заряд «вредных» молекул должен быть выше, чем у «правильных».
Согласно закону Кулона это выливается в притяжение зарядов, то есть наличие большего по величине отрицательного заряда расположенного ближе к стенке сдвинет в этом направлении положительную частицу, а согласно предлагаемой в модели интерпретации это однозначно трактуется как уменьшение внутренней мотивации ученика.
Фактически, это подводит нас к мысли, что для многих качественных оценок нам важно не точное положение частицы в трёхмерных координатах, а высота и расстояние от центра трубы. Поэтому правила взаимодействия Частиц и Вредных Молекул стоит уточнить:
0) И молекула, и частица характеризуются длиной радиус–вектора, т.е. расстоянием от центра. Можно использовать как абсолютные величины, так и относительные.
1) Пока положим, что вредное влияние оказывают только молекулы вредных знаний более удалённые от центра, то есть $r_\mathrm{ВМ}>r_\mathrm{Ч}$. Тем самым мы делаем упор именно на отслеживании вредной информации приходящей извне.
2) Поскольку важен сам эффект притяжения, то сила Кулона рассчитывается для величин зарядов и расстояния $|r_\mathrm{ВМ} - r_\mathrm{Ч}|$. В соответствии с ней происходит перерасчёт радиуса для частицы-ученика.
3) Производится расчёт эффекта диффузии, то есть пересчитывается $r_\mathrm{ВМ}$ с постоянным сдвигом к центру. Поскольку молекулы вредных знаний имеют специальное значение, их взаимодействие с любыми другими молекулами-знаниями (и другими вредными молекулами тоже) не учитывает силу Кулона.
4) Когда оказывается $r_\mathrm{ВМ} \le r_\mathrm{Ч}$, то есть "вредная молекула" достигла уровня мотивации ученика, то возможно имело место столкновение и его надо отработать, предварительно вычислив вероятность её поглощения по текущему уровню внутренней мотивации $r_\mathrm{Ч}$. И только подтвердив столкновение, отработать его как обычно. В противном случае продолжается общий процесс моделирования (вредная молекула продолжает диффундировать к центру трубы, в сторону более мотивированных учеников), и продолжается приведённая последовательность шагов начиная с первого.
5) Достигнув центра, то есть при $r_\mathrm{ВМ}\approx 0$, молекула «уничтожается».
Условие, описанное в пункте один, не является обязательным, так как разделение информации на полезную (обязательную+дополнительную) и вредную в большей степени определяется учителем, как любая активность, не связанная с получением запланированной информации. И если ещё до середины 90х годов XX-го века к внешнему вмешательству больше относилась болтовня в классе, то с развитием информационных технологий полный контроль поступающей информации затруднён. Более того, возможен и «парадокс привлекательности», когда информация была замечена более мотивированными учениками (повлияла на них), но проигнорирована поначалу менее мотивированными. После этого возможны два варианта.
В этой связи и реальность, и многие численные методы так называемой swarm-оптимизации используют понятия поля зрения или радиуса воздействия как граничного значения (threshold value на английском). В том смысле, что только начиная с некоторого расстояния, сила воздействия считается достаточной, чтобы повлиять на указанный элемент. До этого мы его просто не замечаем (один порог чувствительности) или воспринимаем как фоновый шум (другой порог чувствительности).
Таким образом отрабатывается существующий эффект «порога привлекательности» и подобная функциональность заслуживает добавления в модель как элемент, отражающий особенности реальной жизни и процесса обучения.
Но выбор параметров чувствительности это не только вопрос обработки экспериментальных данных для их вычисления. Тот же простейший радиус чувствительности обычно снижается по мере накопления усталости (количества знаний усвоенных на отрезке знаний), то есть прямо пропорционален текущему уровню мотивации. Правда опыт подсказывает, что нелинейно. Так же должен понижаться по мере приближения к пределу скорости обучения данного ученика. А значит неявно зависит и от интенсивности внешних воздействий (фактически любых). Таким образом этот, кажущийся многим малозначимый элемент весьма активно будет влиять на динамику предварительного отбора молекул, так как может как ухудшаться, так и улучшаться по отношению к предполагаемому начальному значению.
Тем самым мы подошли к вопросу упрощённого моделирования эффекта диффузии, ибо влияние сил Кулона вторично. На самом деле в простых учебниках физики можно найти только определение коэффициента диффузии $D$, так как математическая модель процесса очень сложна. Выражаясь простым языком, коэффициент диффузии для нас определяет скорость распространения посторонней информации в среде обучения. И более того, согласно логике нашей модели за некоторое конечное время эта информация достигнет всех (молекула пробежит от края трубы к её центру), а точнее — мы обратим на неё внимание если захотим. Если она не будет поглощена в процессе дрейфа, то как только она окажется в центре, то она уничтожается.
Несмотря на сложность процессов, рассматривая процесс диффузии частиц растворённых в жидкости, можно установить частный результат: средняя дистанция пройденная такой частицей (не нашей модели, а абстрактного физического объекта) равна $\left=\sqrt{6Dt}$, то есть в отличие от механики дистанция пропорциональна квадратному корню из прошедшего времени, но коэффициент пропорциональности однозначно определяется по коэффициенту диффузии.
На самом деле для каждой пары свежепоявившейся молекулы вредных знаний и частицы-ученика эта формула позволяет вычислить время, необходимое на дрейф молекулы к текущей позиции частицы $\sqrt{6Dt}=R-r$ без учёта сил Кулона, то есть $\large t_\mathrm{ожидаемое}=\frac{{(R-r)}^2}{6D}$.
Можно и в безразмерном виде, если необходимо. Это время сознательно названо ожидаемым, так как из-за силы Кулона частица будет двигаться навстречу «вредной молекуле», то есть реальная дистанция будет постепенно уменьшаться. Так как как мы подразумеваем возможность регулярного появления «вредных молекул», то рассчитывать надо суперпозицию сил для множества пока ещё активных молекул с определённым шагом по времени. Поскольку речь идёт о функциональной зависимости, пусть и для среднего «пробега», то скорость перемещения «вредной молекулы» определяется дифференцированием по времени, то есть $\large v_\mathrm{ВМ}(t)=\sqrt{\frac{3D}{2t}}$ и движение в целом можно охарактеризовать как замедленное, так как ускорение равно $\large -\sqrt{\frac{3D}{8t^3}}<0 span="">
Проявлением процесса диффузии будет являться не только уникальное значение её коэффициента для «вброса» каждого нового элемента, но и вероятностные характеристики процесса добавления этих знаний. Эта функциональность модели является независимой надстройкой, и её вероятностные характеристики могут быть разными, то есть в общую модель будут добавлены несколько характеристик, но среди них наверняка будут среднее и разброс в отношении периодичности внедрения молекул знаний извне.
На данный момент мы описываем молекулу знаний триадой <заряд, масса, тип> чтобы отразить изменения в заряде, объёме и плотности частицы. Поэтому, полезные они были или нет, но формально знания потреблены, и масса частицы должна быть скорректирована. Причём как обычно, так как разделение на полезные или вредные может быть ученику неизвестно и с формальной точки зрения объём и/или глубина его знаний изменились.
 |
| В современном мире и прямо на уроке ученик скорее ищет и знакомится с интересной ему информацией, только с современной ювенальной юстицией попробуй, его накажи. И это не плач преподавателя, а о "неминуемости" поглощения учеником любой информации которая не просто попалась ему на глаза, а показалась интересной. Интересней обязательных знаний. |
Согласно закону Кулона это выливается в притяжение зарядов, то есть наличие большего по величине отрицательного заряда расположенного ближе к стенке сдвинет в этом направлении положительную частицу, а согласно предлагаемой в модели интерпретации это однозначно трактуется как уменьшение внутренней мотивации ученика.
Фактически, это подводит нас к мысли, что для многих качественных оценок нам важно не точное положение частицы в трёхмерных координатах, а высота и расстояние от центра трубы. Поэтому правила взаимодействия Частиц и Вредных Молекул стоит уточнить:
0) И молекула, и частица характеризуются длиной радиус–вектора, т.е. расстоянием от центра. Можно использовать как абсолютные величины, так и относительные.
1) Пока положим, что вредное влияние оказывают только молекулы вредных знаний более удалённые от центра, то есть $r_\mathrm{ВМ}>r_\mathrm{Ч}$. Тем самым мы делаем упор именно на отслеживании вредной информации приходящей извне.
2) Поскольку важен сам эффект притяжения, то сила Кулона рассчитывается для величин зарядов и расстояния $|r_\mathrm{ВМ} - r_\mathrm{Ч}|$. В соответствии с ней происходит перерасчёт радиуса для частицы-ученика.
3) Производится расчёт эффекта диффузии, то есть пересчитывается $r_\mathrm{ВМ}$ с постоянным сдвигом к центру. Поскольку молекулы вредных знаний имеют специальное значение, их взаимодействие с любыми другими молекулами-знаниями (и другими вредными молекулами тоже) не учитывает силу Кулона.
4) Когда оказывается $r_\mathrm{ВМ} \le r_\mathrm{Ч}$, то есть "вредная молекула" достигла уровня мотивации ученика, то возможно имело место столкновение и его надо отработать, предварительно вычислив вероятность её поглощения по текущему уровню внутренней мотивации $r_\mathrm{Ч}$. И только подтвердив столкновение, отработать его как обычно. В противном случае продолжается общий процесс моделирования (вредная молекула продолжает диффундировать к центру трубы, в сторону более мотивированных учеников), и продолжается приведённая последовательность шагов начиная с первого.
5) Достигнув центра, то есть при $r_\mathrm{ВМ}\approx 0$, молекула «уничтожается».
Условие, описанное в пункте один, не является обязательным, так как разделение информации на полезную (обязательную+дополнительную) и вредную в большей степени определяется учителем, как любая активность, не связанная с получением запланированной информации. И если ещё до середины 90х годов XX-го века к внешнему вмешательству больше относилась болтовня в классе, то с развитием информационных технологий полный контроль поступающей информации затруднён. Более того, возможен и «парадокс привлекательности», когда информация была замечена более мотивированными учениками (повлияла на них), но проигнорирована поначалу менее мотивированными. После этого возможны два варианта.
- В первом менее мотивированные ученики так и проигнорируют эту информацию, словно у молекулы вредных знаний начальное положение было не $R$ (от стенок), а некоторый радиус $0 < R_0 < R$. То есть исходная вредная молекула была поглощена, но сам ученик превратился во вторичный источник, "испустив" вредную молекулу заново. Возможно идентичную исходной, а возможно собственную версию с другими характеристиками, как по информационной ценности, так и привлекательности.
- Во втором варианте интерес «продвинутых» учеников подействует на менее мотивированных (спровоцирует, обычными словами), но опять начальной позицией будет R0. Так как она представляет собой более высокую мотивацию, то такая вторичная молекула вредных знаний будет действовать на более мотивированных учеников одинаково с оригинальной, но не станет невидимой для менее мотивированных, в отличие от исходного варианта. То есть неявная притягательность-пример более мотивированых (успешных) соучеников. Эта вторичная молекула начнёт тянуть частицы «плохих» учеников к центру, фактически повышая мотивацию всех их (может и только части, в педагогике варианты распространения привлекательности разные), только тут не только вероятность освоения этой информации не обязательно единица, но и сначала "плохой" ученик должен догнать эту вторичную молекулу пока она продолжает диффундировать к центру. То есть шанс усвоить информацию при таком сценарии невелик, но хоть уровень мотивированности косвенно повысится.
В этой связи и реальность, и многие численные методы так называемой swarm-оптимизации используют понятия поля зрения или радиуса воздействия как граничного значения (threshold value на английском). В том смысле, что только начиная с некоторого расстояния, сила воздействия считается достаточной, чтобы повлиять на указанный элемент. До этого мы его просто не замечаем (один порог чувствительности) или воспринимаем как фоновый шум (другой порог чувствительности).
 |
| Трактовки некоторых терминов в технических и гуманитарных отраслях знаний могут иметь специфику |
В трёхмерном пространстве этот эффект обычно реализуется на основе условной сферы с центром в «управляющем» объекте и радиусом чувствительности. Но могут использоваться цилиндры или прямоугольные параллелепипеды (в рамках моей модели это скорее очень тонкий цилиндр (диск радиуса трубы, но не заходящий вперёд, то есть смотрим только на "догоняющие" молекулы знаний).Их размерности также становятся параметрами модели и могут заметно скорректировать её функционирование (по умолчанию применяются для молекул-знаний любого вида). Хотя при разделении полезных знаний на теоретические и практические (или другая подобная классификация) стоит использовать различные границы чувствительности, ибо ученики могут иметь определённые склонности, когда предпочтение практических знаний, например сопровождается не просто лучшим усвоением, но и большей чувствительностью к наличию таковых в учебных материалах.
Но выбор параметров чувствительности это не только вопрос обработки экспериментальных данных для их вычисления. Тот же простейший радиус чувствительности обычно снижается по мере накопления усталости (количества знаний усвоенных на отрезке знаний), то есть прямо пропорционален текущему уровню мотивации. Правда опыт подсказывает, что нелинейно. Так же должен понижаться по мере приближения к пределу скорости обучения данного ученика. А значит неявно зависит и от интенсивности внешних воздействий (фактически любых). Таким образом этот, кажущийся многим малозначимый элемент весьма активно будет влиять на динамику предварительного отбора молекул, так как может как ухудшаться, так и улучшаться по отношению к предполагаемому начальному значению.
 |
| Как согласовать некоторые результаты психологов с уже введёнными параметрами модели? Пока отложено, но вполне ожидаемо что зависимость от того же уровня внутренней мотивации будет кусочно-определённой со своими, пока неизвестными порогами (скорее всего выраженные как относительные величины) |
 |
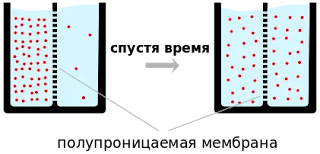| Так это выглядит в теории для идеальных газов и жидкостей |
На самом деле для каждой пары свежепоявившейся молекулы вредных знаний и частицы-ученика эта формула позволяет вычислить время, необходимое на дрейф молекулы к текущей позиции частицы $\sqrt{6Dt}=R-r$ без учёта сил Кулона, то есть $\large t_\mathrm{ожидаемое}=\frac{{(R-r)}^2}{6D}$.
Можно и в безразмерном виде, если необходимо. Это время сознательно названо ожидаемым, так как из-за силы Кулона частица будет двигаться навстречу «вредной молекуле», то есть реальная дистанция будет постепенно уменьшаться. Так как как мы подразумеваем возможность регулярного появления «вредных молекул», то рассчитывать надо суперпозицию сил для множества пока ещё активных молекул с определённым шагом по времени. Поскольку речь идёт о функциональной зависимости, пусть и для среднего «пробега», то скорость перемещения «вредной молекулы» определяется дифференцированием по времени, то есть $\large v_\mathrm{ВМ}(t)=\sqrt{\frac{3D}{2t}}$ и движение в целом можно охарактеризовать как замедленное, так как ускорение равно $\large -\sqrt{\frac{3D}{8t^3}}<0 span="">
Проявлением процесса диффузии будет являться не только уникальное значение её коэффициента для «вброса» каждого нового элемента, но и вероятностные характеристики процесса добавления этих знаний. Эта функциональность модели является независимой надстройкой, и её вероятностные характеристики могут быть разными, то есть в общую модель будут добавлены несколько характеристик, но среди них наверняка будут среднее и разброс в отношении периодичности внедрения молекул знаний извне.
Комментарии
Отправить комментарий